Intuition Behind the Birthday Paradox

The birthday problem refers to a family of statistical problems regarding the computation of various types the probability related to groups of people having the same birthday. For example, it could be about computing the chance of finding two people with the same date of birth in a group of fixed size. Or it could be about finding out the minimum number of people in the same group that gives a probability of at least 50% that two people share the same birthday.

Regardless of the variant, this problem must be solved using basic tool in statistics and combinatorics such as the binomial coefficients. Let’s start by defining these basic elements that we will need to find the solution of the birthday problem.

Background

• Ordered lists with replacement or Exponential: this is the classical way to find the number of possible ways to arrange \(n\) numers (or items) in groups of \(k\) using the formula \(n^k\). By “ordered” we mean here that the order matters and that \(\{1, 2\}\) is not the same as \(\{2, 1\}\). By “replacement” we mean that a number, after being drawn once it can be drawn again. It is, therefore, possible to have samples such as \(\{1, 1\}\) or \(\{2, 2\}\).

• Factorial: this is a special matematical operator, denoted by the question mark “\(!\)”, only defined for integer numbers, that consists in multiplying a given number for all its smaller positive integers:
  $$ n! = n \cdot (n-1) \cdot (n-2) \dots \cdot 2 \cdot 1$$
  The factorial of 3, denoted by \(3!\), will be \(3 \cdot 2 \cdot 1 = 6\). This is used in combinatorics to compute the number of all the possible ways to order a set of given size. If you have a set of \(n\) elements, for example, its items can be ordered in \(n!\) ways.
• Ordered lists without replacement or Permutations \(\mathcal{P}(n,k)\): this term refers to all the possible ways to arrange a set of \(n\) elements in ordered groups of size \(k\).
  The permutation formula is:
  $$ \mathcal{P}(n,k) = \frac{n!}{(n-k)!} = n \cdot (n-1) \cdot (n-2) \dots (n-k+1)$$
  In the special case which \(k = n\) we can see that \(\mathcal{P}(n,n)\) simply corresponds to the factorial \(n!\).
• Unordered lists without replacement or Combinations \(\mathcal{C}(n,k)\) (or “binomial coefficient”) is the set of all the possible unordered groups of size \(k\) in which a set of \(n\) elements can be arranged. As we have seen above, \(k!\) is the number of all possible ways to order a group of \(k\) elements. To find \(\mathcal{C}(n,k)\) it is, therefore, enough to take the equation for \(\mathcal{P}(n,k)\) and divide it by \(k!\):

$$ \mathcal{C}(n,k) = {n \choose k} = \frac{n!}{k! \cdot (n-k)!} $$

Frequentist Approach to Statistics

There are mainly two approaches to statistics: Bayesian and frequentist. The former is usually followed when we have a prior knowledge about the problem we are trying to solve which might help us find the solution faster. In the case of the birthday problem, however, we don’t have any such prior so we will follow the latter approach, which consists of counting how many times a given event occurs.

To find a probability of an event in this way, we have to compute the ratio between the number of all possible ways in which the event can occur, divided by the whole population. If we want to find the probability of getting less than \(3\) when we roll a fair die, for example, the cardinality (i.e. the size) of the set of possible ways in which the event \(E\) can occur is 2 (\(E = \{ 1, 2\}\)) and the size of the total population \(P = \{ 1, 2, 3, 4, 5, 6\}\) is 6. The probability \(P(E)\) is, therefore, \(2/6\). In general, we have that:

$$ P(E) = \frac{|E|}{|P|} $$

Where \(|\cdot|\) denotes the cardinality of the set.

Birthday Problem Solution

Going back to the our original birthday problem, we want to find the minimum party size \(N\) which will give us a probability of at least 50% to find two people with the same birthday. We define this as the event \(B\).

A key trick to find the correct solution is to look for the solution opposite event \(\bar{B}\), namely: what is the number of people which will give us a probability of less than 50% to find no couple of people with the same birthday?

This is easier to solve than the original problem because we have a ready made equation that can provide us just what we want, the permutations \(\mathcal{P}(n,k)\). Because this rules out replacements, for \(n=365\) and \(k=N\), this will give us the number of possible sets of \(N\) people that were not born on the same day.

Once we have found the probability for this \(\bar{B}\), it’s then easy to find \(P(B)\) (the complementary probability) as the two events are mutually exclusive and, therefore, \(P(B) + P(\bar{B}) = 1\).

$$ P(\bar{B}) = \frac{\mathcal{P}(n=365,k=N)}{365^N}$$

\(N\) is our free variable that represents the number of people at the birthday party. We can solve for \(N\) graphically if we represent the graph of the function \(P(B) = 1 – P(\bar{B})\) and intersect it with the line \(y=0.5\).

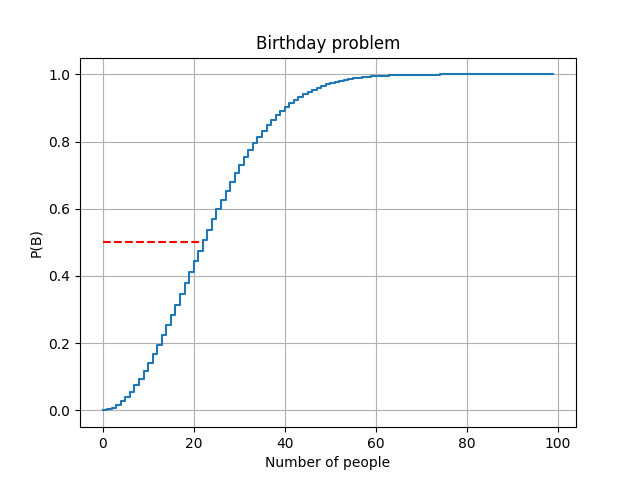
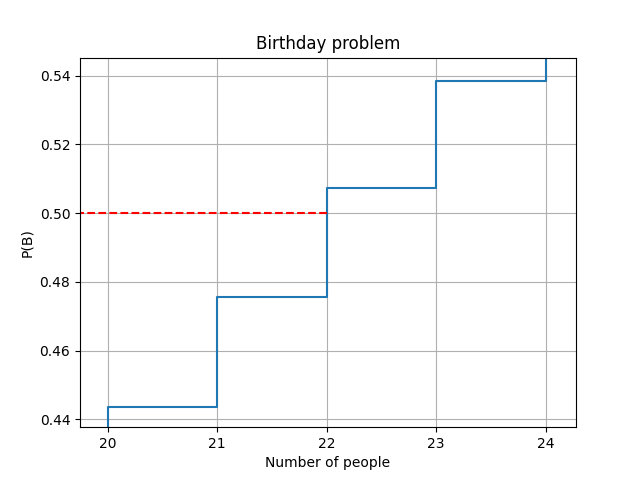
From the plots above we can see that P(B)>0.5 for N>22. Therefore \(N=23\) is the first integer number that provides a probability of more than 50% and is the solution we were looking for!

Isn’t it surprising that we only need 23 people in a group to have a pretty good chance of finding two people with the same birthday?

This is pretty counter-intuitive. A possible explanation for this is that we as humans often tend to misinterpret the Birthday problem and try and find the chances of someone having the same birthday as us! But this is a much more specific problem and it’s not what the birthday problem is about.

“Double Birthday” Problem

Let’s say we want to find how many people we need to gather to have a chance higher than 50% to find someone else with our same birthday. Let’s call this event A and P(A) is the probability that this will occur.

In that case again we want to use the property that \(P(A) = 1 – P(\bar{A})\). \(P(\bar{A})\) represents the chances of finding someone with a different birthday than ours. Its numerator, therefore, will have to account for repeated birthdays, meaning that we must consider replacement in this case.

The equation for \(P(A)\) can therefore be written using the exponential \(364^N\) in the numerator of \(P(\bar{A})\) rather than the permutation \(\mathcal{P}(365,K)\):

$$ P(\bar{A}) = 1 – \frac{364^N}{365^N} = 1 – \left( \frac{364}{365} \right)^N$$

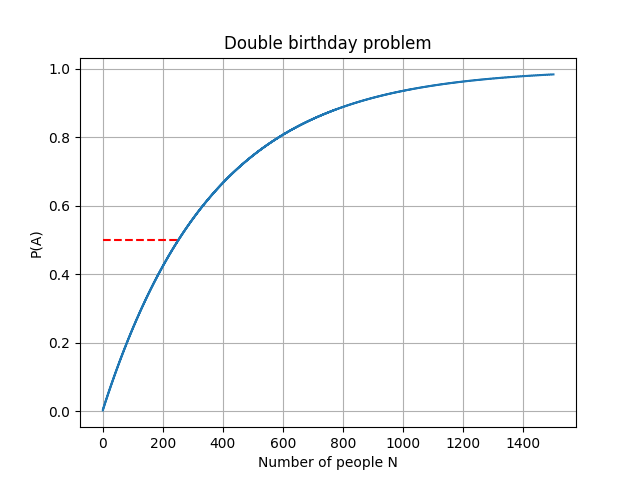
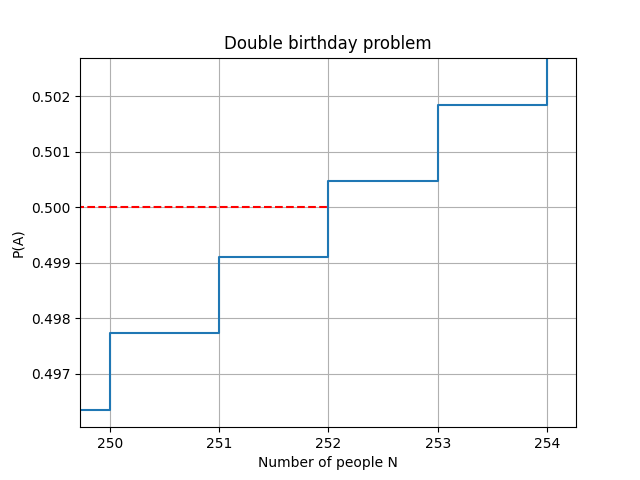
As you can see from the plots above, you need to have 253 people in order to have a chance of at least 50% to find another guest at your birthday party also celebrating their birthday on the same day! This is a much a higher number than the original birthday problem that we saw above, which matches more with our intuition!

Code

• You can find a Jupyter Notebook with easy-to-use code to replicate the plots shown above in GitHub.

References

• Counting and combinatorics